жӢүжў…зҡ„科еӯҰиҙЎзҢ®дёҺж•°еӯҰжҖқжғіеҜ№иҝ‘д»Је·ҘзЁӢеҠӣеӯҰеҸ‘еұ•зҡ„ж·ұиҝңеҪұе“Қ
еҠ еёғйҮҢеҹғе°”В·жӢүжў…пјҲGabriel LamГ©пјҢ1795вҖ”1870пјүжҳҜжі•еӣҪи‘—еҗҚзҡ„ж•°еӯҰ家дёҺзү©зҗҶеӯҰ家пјҢд»–зҡ„з ”з©¶жҲҗжһңжЁӘи·Ёж•°еӯҰгҖҒзү©зҗҶеӯҰдёҺе·ҘзЁӢ科еӯҰзӯүеӨҡдёӘйўҶеҹҹпјҢеҜ№иҝ‘д»Је·ҘзЁӢеҠӣеӯҰзҡ„еҘ еҹәдёҺеҸ‘еұ•дә§з”ҹдәҶж·ұиҝңеҪұе“ҚгҖӮжң¬ж–Үе°Ҷд»ҘвҖңжӢүжў…зҡ„科еӯҰиҙЎзҢ®дёҺж•°еӯҰжҖқжғіеҜ№иҝ‘д»Је·ҘзЁӢеҠӣеӯҰеҸ‘еұ•зҡ„ж·ұиҝңеҪұе“ҚвҖқдёәдё»йўҳпјҢд»ҺеӣӣдёӘж–№йқўеұ•ејҖи®әиҝ°гҖӮйҰ–е…ҲпјҢжҺўи®Ёд»–еңЁеј№жҖ§еҠӣеӯҰдёҺеә”еҠӣеҲҶжһҗдёӯзҡ„ејҖеҲӣжҖ§иҙЎзҢ®пјҢйҳҗжҳҺе…¶вҖңжӢүжў…ж–№зЁӢвҖқдёҺвҖңжӢүжў…еёёж•°вҖқеңЁжқҗж–ҷеҠӣеӯҰдёӯзҡ„еҹәзЎҖең°дҪҚпјӣе…¶ж¬ЎпјҢеҲҶжһҗд»–еңЁжӣІзәҝеқҗж Үзі»дёҺжӨӯеңҶеҮҪж•°ж–№йқўзҡ„ж•°еӯҰжҖқжғіпјҢжҸӯзӨәе…¶еҜ№еӨҚжқӮз»“жһ„еҲҶжһҗж–№жі•зҡ„еҪұе“Қпјӣ第дёүпјҢд»Ӣз»Қд»–еңЁе·ҘзЁӢе®һи·өдёҺзҗҶи®әз»“еҗҲдёӯзҡ„еҲӣж–°пјҢе°Өе…¶жҳҜеңЁжЎҘжўҒгҖҒеҺӢеҠӣе®№еҷЁзӯүе·ҘзЁӢи®ҫи®Ўдёӯзҡ„еә”з”ЁпјӣжңҖеҗҺпјҢжҺўи®ЁжӢүжў…жҖқжғіеңЁзҺ°д»Је·ҘзЁӢеҠӣеӯҰдёҺи®Ўз®—еҠӣеӯҰдёӯзҡ„延з»ӯдёҺеҸ‘еұ•гҖӮйҖҡиҝҮзі»з»ҹеҲҶжһҗпјҢеҸҜд»ҘзңӢеҲ°жӢүжў…дёҚд»…еҘ е®ҡдәҶиҝ‘д»Је·ҘзЁӢеҠӣеӯҰзҡ„зҗҶи®әеҹәзЎҖпјҢд№ҹд»ҘдёҘеҜҶзҡ„ж•°еӯҰжҖқз»ҙдёәе·ҘзЁӢ科еӯҰзҡ„еҸ‘еұ•жҸҗдҫӣдәҶеқҡе®һж”Ҝж’‘пјҢдҪҝе…¶жҲҗдёәиҝһжҺҘж•°еӯҰдёҺе·ҘзЁӢзҡ„дјҹеӨ§жЎҘжўҒдәәзү©гҖӮ
1гҖҒеј№жҖ§еҠӣеӯҰдёҺеә”еҠӣеҲҶжһҗзҡ„еҘ еҹәдҪңз”Ё
жӢүжў…жңҖи‘—еҗҚзҡ„科еӯҰиҙЎзҢ®д№ӢдёҖпјҢжҳҜд»–еңЁеј№жҖ§еҠӣеӯҰйўҶеҹҹжҸҗеҮәзҡ„вҖңжӢүжў…ж–№зЁӢвҖқе’ҢвҖңжӢүжў…еёёж•°вҖқгҖӮиҝҷдёӨйЎ№жҲҗжһңжһ„жҲҗдәҶзәҝжҖ§еј№жҖ§зҗҶи®әзҡ„ж ёеҝғпјҢжҲҗдёәз ”з©¶еӣәдҪ“еҠӣеӯҰдёҺжқҗж–ҷеҸҳеҪўи§„еҫӢзҡ„еҹәжң¬е·Ҙе…·гҖӮйҖҡиҝҮе®ҡд№үжқҗж–ҷзҡ„дёӨдёӘзӢ¬з«Ӣеёёж•°пјҢжӢүжў…дҪҝеҫ—еј№жҖ§й—®йўҳзҡ„ж•°еӯҰеҢ–жҲҗдёәеҸҜиғҪпјҢдёәеҗҺжқҘзҡ„еә”еҠӣеҲҶжһҗеҘ е®ҡдәҶзІҫзЎ®зҡ„зҗҶи®әжЎҶжһ¶гҖӮ
еңЁз ”究еҗ„еҗ‘еҗҢжҖ§еј№жҖ§дҪ“зҡ„е№іиЎЎй—®йўҳж—¶пјҢжӢүжў…е°Ҷеҫ®еҲҶж–№зЁӢж–№жі•еј•е…Ҙе·ҘзЁӢеҲҶжһҗд№ӢдёӯпјҢдҪҝеҫ—еә”еҠӣдёҺеә”еҸҳд№Ӣй—ҙзҡ„е…ізі»еҫ—д»Ҙзі»з»ҹеҢ–жҸҸиҝ°гҖӮиҝҷдёҖж–№жі•дёәе·ҘзЁӢеёҲжҸҗдҫӣдәҶеҲҶжһҗеӨҚжқӮиҪҪиҚ·жғ…еҶөдёӢжқҗж–ҷе“Қеә”зҡ„еҹәзЎҖгҖӮдҫӢеҰӮпјҢеңЁеҺӢеҠӣе®№еҷЁгҖҒз®ЎйҒ“д»ҘеҸҠең°еЈіеә”еҠӣеҲҶжһҗдёӯпјҢжӢүжў…е…¬ејҸиҮід»Ҡд»ҚжҳҜз»Ҹе…ёзҡ„и§ЈжһҗжЁЎеһӢгҖӮ
жӢүжў…зҡ„е·ҘдҪңдёҚд»…йҷҗдәҺзҗҶи®әжҺЁеҜјпјҢд»–иҝҳжіЁйҮҚдёҺе·ҘзЁӢй—®йўҳзҡ„з»“еҗҲгҖӮд»–жҸҗеҮәзҡ„вҖңеҺҡеЈҒеңҶзӯ’е…¬ејҸвҖқйҰ–ж¬ЎеҮҶзЎ®жҸҸиҝ°дәҶеҶ…еӨ–еҺӢеҠӣдҪңз”ЁдёӢзҡ„еә”еҠӣеҲҶеёғ规еҫӢпјҢиҝҷдёҖжҲҗжһңжҲҗдёәзҺ°д»Је·ҘзЁӢи®ҫи®Ўзҡ„йҮҢзЁӢзў‘пјҢе№ҝжіӣз”ЁдәҺиҲӘз©әгҖҒжңәжў°е’ҢеңҹжңЁе·ҘзЁӢйўҶеҹҹгҖӮеҸҜд»ҘиҜҙпјҢжӢүжў…зҡ„з ”з©¶е®һзҺ°дәҶеҠӣеӯҰзҗҶи®әд»Һз»ҸйӘҢйҳ¶ж®өеҗ‘ж•°еӯҰеҢ–гҖҒ科еӯҰеҢ–зҡ„йҮҚеӨ§и·Ёи¶ҠгҖӮ
2гҖҒжӣІзәҝеқҗж ҮдёҺжӨӯеңҶеҮҪж•°зҡ„ж•°еӯҰеҲӣж–°
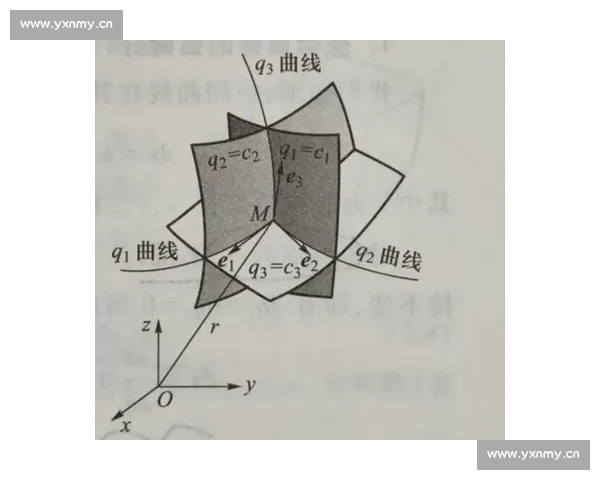
жӢүжў…еңЁж•°еӯҰйўҶеҹҹзҡ„йҖ иҜЈж·ұеҺҡпјҢзү№еҲ«жҳҜеңЁжӣІзәҝеқҗж ҮдёҺжӨӯеңҶеҮҪж•°ж–№йқўзҡ„з ”з©¶пјҢдёәеӨҚжқӮз»“жһ„зҡ„еҠӣеӯҰеҲҶжһҗжҸҗдҫӣдәҶж–°зҡ„ж•°еӯҰе·Ҙе…·гҖӮд»–еј•е…Ҙзҡ„вҖңжӢүжў…еҮҪж•°вҖқпјҲLamГ© functionsпјүеңЁеӨ„зҗҶжӨӯзҗғеҪўе’ҢеңҶжҹұеҪўеқҗж Үзі»й—®йўҳж—¶жһҒе…·еЁҒеҠӣпјҢдҪҝеҫ—еӨҚжқӮеҮ дҪ•иҫ№з•ҢдёӢзҡ„еј№жҖ§й—®йўҳеҸҜд»Ҙеҫ—еҲ°зІҫзЎ®жұӮи§ЈгҖӮ
иҝҷдёҖж•°еӯҰеҲӣж–°жһҒеӨ§ең°жҺЁеҠЁдәҶе·ҘзЁӢи®Ўз®—зҡ„зІҫеәҰгҖӮдј з»ҹз¬ӣеҚЎе°”еқҗж Үйҡҫд»Ҙеә”еҜ№еӨҚжқӮиҫ№з•ҢжқЎд»¶пјҢиҖҢжӢүжў…зҡ„жӣІзәҝеқҗж ҮжҖқжғідҪҝеҫ—е·ҘзЁӢеёҲиғҪеӨҹжӣҙиҮӘ然ең°иЎЁиҫҫз»“жһ„зҡ„зңҹе®һеҮ дҪ•зү№еҫҒпјҢд»ҺиҖҢжҸҗй«ҳдәҶеҲҶжһҗз»“жһңзҡ„еҸҜйқ жҖ§дёҺе®һз”ЁжҖ§гҖӮ
жӯӨеӨ–пјҢжӢүжў…еңЁж•°еӯҰе»әжЁЎдёҠзҡ„дёҘи°ЁжҖқжғіпјҢдёәеҗҺжқҘзҡ„и®Ўз®—еҠӣеӯҰеҸ‘еұ•жҸҗдҫӣдәҶзҗҶи®әж”ҜжҢҒгҖӮд»–ејәи°ғж–№зЁӢзҡ„еҜ№з§°жҖ§дёҺиҫ№з•ҢжқЎд»¶зҡ„йҮҚиҰҒжҖ§пјҢиҝҷз§Қж•°еӯҰжҖқжғіеҗҺжқҘиў«е№ҝжіӣеә”з”ЁдәҺжңүйҷҗе…ғжі•дёҺж•°еҖјжЁЎжӢҹд№ӢдёӯпјҢдҪҝеҫ—е·ҘзЁӢеҠӣеӯҰй—®йўҳд»Һи§Јжһҗи§Јеҗ‘и®Ўз®—и§Јзҡ„иҝҮжёЎжӣҙдёәйЎәз•…гҖӮ
3гҖҒзҗҶи®әдёҺе·ҘзЁӢе®һи·өзҡ„иһҚеҗҲжҺўзҙў
жӢүжў…дёҚд»…жҳҜдёҖдҪҚзҗҶи®ә科еӯҰ家пјҢжӣҙжҳҜдёҖдҪҚе…·жңүе·ҘзЁӢе®һи·өзІҫзҘһзҡ„ж•°еӯҰ家гҖӮд»–жӣҫеңЁжі•еӣҪзҡ„й“Ғи·ҜдёҺжЎҘжўҒе»әи®ҫдёӯжӢ…д»»йЎҫй—®пјҢиҮҙеҠӣдәҺе°Ҷж•°еӯҰж–№жі•еә”з”ЁдәҺе·ҘзЁӢи®ҫи®ЎгҖӮиҝҷз§ҚвҖңзҗҶи®әжңҚеҠЎе·ҘзЁӢвҖқзҡ„зҗҶеҝөпјҢдҪҝд»–зҡ„з ”з©¶жҲҗжһңе…·жңүжһҒй«ҳзҡ„зҺ°е®һд»·еҖјгҖӮ
д»–еңЁжЎҘжўҒжӢұеҪўз»“жһ„еҲҶжһҗдёӯйҰ–ж¬Ўиҝҗз”ЁдәҶеј№жҖ§зҗҶи®әпјҢжҸҗеҮәдәҶд»Ҙеә”еҠӣеҲҶеёғдёәдҫқжҚ®зҡ„з»“жһ„дјҳеҢ–ж–№жі•гҖӮиҝҷз§Қж–№жі•зӘҒз ҙдәҶд»ҘеҫҖдҫқйқ з»ҸйӘҢи®ҫи®Ўзҡ„жЁЎејҸпјҢдҪҝе·ҘзЁӢи®ҫи®ЎйҖҗжӯҘиҝҲеҗ‘科еӯҰеҢ–дёҺе®ҡйҮҸеҢ–гҖӮжӢүжў…зҡ„жҖқжғід№ҹзӣҙжҺҘеҪұе“ҚдәҶеҗҺжқҘзҡ„з»“жһ„еҠӣеӯҰзҗҶи®әпјҢеҢ…жӢ¬ејҜжӣІгҖҒжүӯиҪ¬е’ҢеұҲжӣІзӯүй—®йўҳзҡ„зі»з»ҹеҲҶжһҗгҖӮ
еңЁе·ҘзЁӢж•ҷиӮІж–№йқўпјҢжӢүжў…з§ҜжһҒжҺЁеҠЁж•°еӯҰдёҺеҠӣеӯҰиҜҫзЁӢзҡ„з»“еҗҲпјҢејәи°ғ科еӯҰи®ӯз»ғдёҺе®һи·өиғҪеҠӣзҡ„з»ҹдёҖгҖӮд»–зҡ„ж•ҷеӯҰжҖқжғіеҗҺжқҘжҲҗдёәжі•еӣҪе·ҘзЁӢж•ҷиӮІдҪ“зі»зҡ„йҮҚиҰҒеҹәзҹіпјҢд№ҹдёәе…Ёзҗғе·ҘзЁӢеҠӣеӯҰж•ҷиӮІжЁЎејҸзҡ„еҪўжҲҗжҸҗдҫӣдәҶиҢғдҫӢгҖӮ
4гҖҒеҜ№зҺ°д»Је·ҘзЁӢдёҺи®Ўз®—еҠӣеӯҰзҡ„ж·ұиҝңеҪұе“Қ
иҝӣе…ҘдәҢеҚҒдё–зәӘеҗҺпјҢжӢүжў…зҡ„жҖқжғіеңЁзҺ°д»Је·ҘзЁӢдёҺи®Ўз®—еҠӣеӯҰдёӯз„•еҸ‘еҮәж–°зҡ„з”ҹе‘ҪеҠӣгҖӮжңүйҷҗе…ғжі•гҖҒиҫ№з•Ңе…ғжі•зӯүж•°еҖјеҲҶжһҗжҠҖжңҜзҡ„еҸ‘еұ•пјҢжң¬иҙЁдёҠйғҪе»әз«ӢеңЁжӢүжў…жҸҗеҮәзҡ„еј№жҖ§зҗҶи®әдёҺеҒҸеҫ®еҲҶж–№зЁӢжЁЎеһӢд№ӢдёҠгҖӮеҸҜд»ҘиҜҙпјҢзҺ°д»Је·ҘзЁӢеҲҶжһҗзҡ„жҜҸдёҖдёӘи®Ўз®—жЁЎеқ—пјҢйғҪиғҪжүҫеҲ°жӢүжў…зҗҶи®әзҡ„еҪұеӯҗгҖӮ
еңЁжқҗж–ҷ科еӯҰйўҶеҹҹпјҢжӢүжў…ж–№зЁӢиў«иҝӣдёҖжӯҘжү©еұ•з”ЁдәҺеӨҚеҗҲжқҗж–ҷгҖҒзғӯеј№жҖ§е’ҢеЎ‘жҖ§еҠӣеӯҰеҲҶжһҗдёӯпјҢжҲҗдёәжҸҸиҝ°еӨҡе°әеәҰгҖҒеӨҡзү©зҗҶиҖҰеҗҲй—®йўҳзҡ„йҮҚиҰҒеҹәзЎҖгҖӮиҝҷз§Қи·ЁеӯҰ科зҡ„еә”з”ЁпјҢжӯЈдҪ“зҺ°дәҶжӢүжў…зҗҶи®әзҡ„ејҖж”ҫжҖ§дёҺжҢҒд№…з”ҹе‘ҪеҠӣгҖӮ
жӣҙдёәйҮҚиҰҒзҡ„жҳҜпјҢжӢүжў…дёҘи°Ёзҡ„ж•°еӯҰйҖ»иҫ‘дёҺеҜ№иҮӘ然规еҫӢзҡ„жҠҪиұЎиЎЁиҫҫпјҢжҲҗдёә科еӯҰз ”з©¶ж–№жі•и®әзҡ„йҮҚиҰҒе…ёиҢғгҖӮд»–зҡ„жҖқжғіжҸҗйҶ’еҗҺдәәпјҢ科еӯҰеҲӣж–°еҝ…йЎ»з«Ӣи¶ідәҺзІҫзЎ®зҡ„ж•°еӯҰжҺЁзҗҶдёҺе®һи·өйӘҢиҜҒзҡ„з»ҹдёҖпјҢиҝҷдёҖзҗҶеҝөиҮід»Ҡд»Қеј•еҜјзқҖе·ҘзЁӢеҠӣеӯҰдёҺеә”з”Ёж•°еӯҰзҡ„еүҚиЎҢж–№еҗ‘гҖӮ
жҖ»з»“пјҡ
lewin乐玩,乐玩lehu唯一官网,Lewin,乐玩LEWIN-乐玩国际з»јдёҠжүҖиҝ°пјҢжӢүжў…д»Ҙе…¶ж·ұйӮғзҡ„ж•°еӯҰжҖқжғіе’ҢдёҘеҜҶзҡ„科еӯҰзІҫзҘһпјҢеҘ е®ҡдәҶиҝ‘д»Је·ҘзЁӢеҠӣеӯҰзҡ„зҗҶи®әеҹәзЎҖгҖӮд»–дёҚд»…дёәеј№жҖ§еҠӣеӯҰе»әз«ӢдәҶзі»з»ҹзҡ„ж•°еӯҰжЁЎеһӢпјҢиҝҳе°ҶжӣІзәҝеқҗж ҮдёҺеҮҪж•°еҲҶжһҗеј•е…Ҙе·ҘзЁӢи®Ўз®—пјҢжһҒеӨ§жӢ“еұ•дәҶеҠӣеӯҰз ”з©¶зҡ„ж·ұеәҰдёҺе№ҝеәҰгҖӮ
жӣҙдёәж·ұиҝңзҡ„жҳҜпјҢжӢүжў…д»Ҙж•°еӯҰдёәжЎҘжўҒпјҢе®һзҺ°дәҶ科еӯҰзҗҶи®әдёҺе·ҘзЁӢе®һи·өзҡ„е®ҢзҫҺз»“еҗҲгҖӮд»–зҡ„жҖқжғіеҪұе“ҚдәҶеҗҺдё–зҡ„и®Ўз®—еҠӣеӯҰгҖҒз»“жһ„е·ҘзЁӢд№ғиҮіжқҗж–ҷ科еӯҰзҡ„еҸ‘еұ•ж–№еҗ‘пјҢжҲҗдёәиҝһжҺҘж•°еӯҰдёҺе·ҘзЁӢ科еӯҰзҡ„дјҹеӨ§е…Ҳй©ұгҖӮд»ҠеӨ©пјҢеҪ“жҲ‘们еңЁй«ҳжҖ§иғҪи®Ўз®—дёҺжҷәиғҪи®ҫи®Ўзҡ„ж—¶д»ЈеӣһжңӣеҺҶеҸІпјҢжӢүжў…зҡ„еҗҚеӯ—дҫқж—§й—ӘиҖҖзқҖзҗҶжҖ§дёҺеҲӣж–°зҡ„е…үиҫүгҖӮ